 Rys.1
Rys.1
Zmienna to symboliczna reprezentacja cechy badanego obiektu lub procesu. Tak więc każda zmienna występuje w postaci swojej nazwy lub innego symbolu (np. greckiej litery) i reprezentuje wartość określonej cechy mierzalnej (np.: wartości siły obciążenia w Newtonach czy temperatury w stopniach) lub cechę niemierzalną (np.: nazwę maszyny).
Modele matematyczne wyrażają - w postaci funkcji oraz równań i nierówności - zależności między interesującymi badacza zmiennymi. Zmienne, których wartości zadajemy to zmienne wejściowe, natomiast te zmienne, których zachowanie badamy nazywane są zmiennymi wyjściowymi.
Należy pamiętać, że każdy model odwzorowuje tylko niektóre, wybrane cechy rzeczywistego obiektu czy procesu i to najczęściej w sposób uproszczony (np.: liniowy zamiast nieliniowego) i ograniczony do określonych zakresów wartości zmiennych wejściowych (np.: w zakresie odkształceń sprężystych).
Zmienne DYSKRETNE (czyli skokowe) przyjmują tylko określone wartości ze skończonego lub przeliczalnego zbioru (np.: liczba zębów, liczba uszkodzeń, znormalizowana średnica)
Zmienne CIĄGŁE - posiadają nieskończenie wiele wartości w każdym dowolnym skończonym przedziale. Przykłady: siła, temperatura, naprężenie
W praktyce - przy ograniczonej dokładności pomiaru i określonej precyzji zapisu cyfrowego - zmienne ciągłe ulegają dyskretyzacji.
Powszechnie spotykane zmienne deterministyczne to zmienne, które mają zawsze określoną wartość, ponieważ:
- dla zmiennych wejściowych konkretne wartości są dane,
- wartości zmiennych wyjściowych są jednoznacznie obliczane na podstawie tych danych oraz wzorów.
Modele deterministyczne nie uwzględniają więc losowego rozrzutu wartości zmiennych.
W praktyce często występuje jednak wpływ zakłóceń, błędów i innych czynników nie pozwalających ani precyzyjnie i w sposób powtarzalny zadawać wartości zmiennych wejściowych ani wyznaczać wartości zmiennych wyjściowych. Inaczej mówiąc - wartości zmiennych wykazują losowy rozrzut.
Zmienne losowe to zmienne, których konkretnych wartości nigdy nie możemy ustalić ani przwidzieć, jednak aby móc je badać i tworzyć statystyczne modele matematyczne
musimy znać ich rozkłady prawdopodobieństwa.
Inaczej mówiąc - musimy dla każdej zmiennej losowej znać granice zakresu w jakim mogą
występować jej wartości oraz znać
prawdopodobieństwo występowania różnych wartości tej zmiennej.
Modele statystyczne (zwane też stochastycznymi) mają pomóc użytkownikowi określać prawdopodobieństwo różnych zdarzeń - w naszych przypadkach - związanych z eksploatacją maszyn i urządzeń, na przykład przekroczenia dopuszczalnych obciążeń czy naprężeń. Modele te bazują na teoretycznych rozkładach prawdopodobieństwa dobranych dla poszczególnych zmiennych losowych tak aby jak najlepiej odzwierciedlić ich rzeczywiste zachowanie. Bardziej zaawansowane modele badają także zmienność tych rozkładów w czasie czyli procesy stochastyczne a więc ich głównie dotyczy nazwa "modele stochastyczne"
Rozkłady zmiennych losowych można uzyskać:Na podstawie przeprowadzonej dostatecznie dużej liczby pomiarów zmiennej losowej otrzymujemy dane statystyczne i sporządzamy histogram.
Przykład 1:
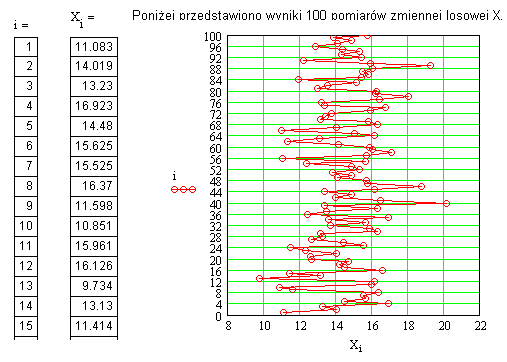
Wykonano 100 pomiarów pewnej zmiennej X. Wartości tych pomiarów zaznaczono punktami na wykresie poniżej, przy czym na osi pionowej są numery pomiarów a na osi poziomej wartości zmiennej losowej X.
Jak widać, uzyskane z pomiaru wartości mieszczą się w zakresie od 8 do 22.
 Rys.1
Rys.1
Dla oszacowania częstości występowania wartości zmiennej losowej X z różnych przedziałów zakresu jej zmienności, sporządzimy histogram.
Histogram przedstawiany jest jako wykres słupkowy, przy czym na osi poziomej jest zakres zmienności zmiennej losowej podzielony na M równych przedziałów, a każdemu z nich odpowiada słupek o wysokości równej liczbie pomiarów, których wartość zmieściła się w tym przedziale.
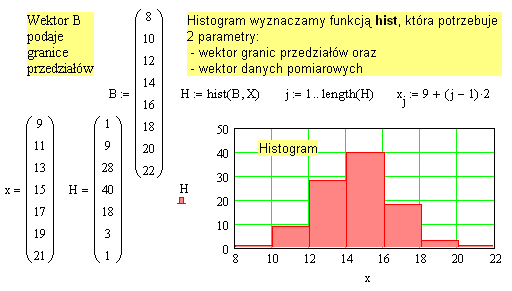
W naszym przypadku, patrząc na rys.1, dzielimy cały zakres <8; 22> na 7 przedziałów o długości 2
i definiujemy to jako wektor granic przedziałów B, a następnie wykorzystujemy w Mathcadzie funkcję
hist.
 Rys.2
Rys.2
Porównując rysunki 1 i 2 widzimy, że każdy słupek histogramu ma wysokość równą sumie punktów zawartych na Rys.1 w pionowym pasie odpowiadającym przedziałowi przypisanemu temu słupkowi.
Zamiast funkcji hist można zastosować w Mathcadzie funkcję histogram, której jako pierwszy parametr wystarczy podać liczbę słupków (Rys.3).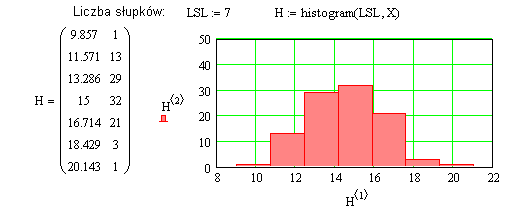 Rys.3
Rys.3Przykład 2:
|
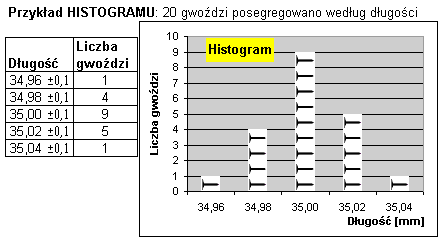
Jeśli mamy zbiór 20 gwoździ o nominalnej długości 35 mm, to po zmierzeniu każdego okaże się, że rzeczywista długość gwoździa jest w tym zbiorze zmienną losową. Jej histogram otrzymamy np. po rozdzieleniu gwoździ na grupy według przedziałów długości. |
Jeśli obwiednia wierzchołków słupków histogramu ma bardzo nieregularny kształt to niewiele więcej można zdziałać. Jeśli natomiast przypomina kształt jakiejś krzywej analitycznej (na przykład krzywej Gauss'a) to warto dopasować taką krzywą czyli dopasować teoretyczny rozkład prawdopodobieństwa (lub gęstości prawdopodobieństwa).
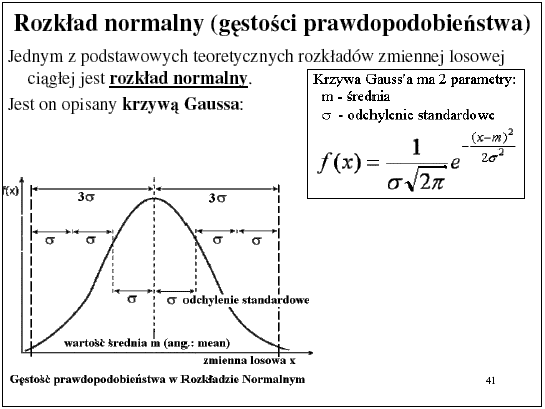
Bardzo często dopasowujemy rozkład normalny. Gęstość rozkładu takiego rozkładu
wyraża się krzywą Gauss'a. Umowne granice tej krzywej [Xmin; Xmax] przyjmujemy w/g tzw.
"reguły trzech sigm": Xmin=Xsr-3*sigma; Xmax=Xsr+3*sigma

O gęstości prawdopodobieństwa mówimy w przypadku zmiennej losowej ciągłej. Z definicji zmienna ciągła to taka, która w każdym skończonym przedziale ma nieskończenie wiele wartości. Prawdopodobieństwo wystąpienia jednej wartości z nieskończenie wielu jest zawsze równe zeru. Dla takiej zmiennej można jedynie określić krzywą dystrybuanty czyli skumulowanego rozkładu prawdopodobieństwa (ang.: CDF = Cumulative Distribution Function).
Krzywą dystrybuanty zmiennej losowej X otrzymujemy mając dla kolejnych jej wartości X=x1, X=x2, X=x3, ... (przy ustalonym przyroście dx) prawdopodobieństwa wystąpienia wartości mniejszych : P(X < x1), P(X < x2), P(X < x3), ... co ogólnie zapisuje się jako: F(x)=P(X < x)
Dowolny słupek histogramu skumulowanego jest sumą wszystkich poprzedzających go słupków histogramu zwykłego.
Mając krzywą dystrybuanty można wyznaczyć jej pochodną czyli gęstość rozkładu prawdopodobieństwa. Skoro gęstość f(x) jest pochodną z dystrybuanty: f(x)=F'(x) to i na odwrót: dystrybuanta F(x) to całka z funkcji gęstości prawdopodobieństwa f(x).
Na wykresach poniżej przedstawiono prawdopodobieństwo P1, że zmienna losowa x przyjmie wartość mniejszą niż x1. Jak widać: na wykresie gęstości prawdopodobieństwa (z lewej) jest to zaznaczone pole pod krzywą Gauss'a, a na wykresie dystrybuanty (z prawej) jest to rzędna P1 punktu na krzywej dystrybuanty odczytana dla odciętej x1:
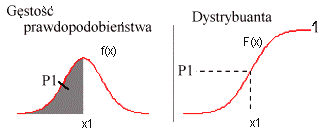
| Całe pole pod krzywą gęstości prawdopodobieństwa wynosi 1, tak samo 1 to maksymalna wartość dystrybuanty. Zamiast wyznaczać pola pod krzywą Gauss'a należy więc odczytywać wartości (rzędne) na krzywej dystrybuanty rozkładu normalnego. |